HABILIDADES MATEMÁTICAS

Aquí puedes encontrar vídeos con las explicaciones de los temas enseñados en clases 

SISTEMA DE NUMERACIÓN DECIMAL

Para expresar los números empleamos una serie de símbolos y unas normas para leerlos, a eso lo llamamos sistema de numeración. En nuestro sistema de numeración empleamos diez cifras diferentes para expresar los valores. Es un sistema posicional porque el valor de una cifra depende de su posición, cada puesto más avanzado hacia la izquierda en que esté una cifra su valor es diez veces más. En un número natural identificamos sus cifras desde la derecha: unidades, vale el valor que representa, decenas, vale 10 veces su valor, centenas, vale 100 veces su valor, unidades de millar, vale 1000 veces su valor, decenas de millar, vale 10000 veces su valor, centenas de millar, vale 100000 veces su valor, unidades de millón, vale 1000000 veces su valor, decenas de millón, vale 10000000 veces su valor, centenas de millón, vale 100000000 veces su valor, ... ... ... A esta manera de expresar los números lo llamamos sistema de numeración decimal.

Los órdenes de unidades de un número natural.

La causa de que empleemos el sistema de numeración decimal es debido a que de siempre se han utilizado los dedos de las manos para contar. Actualmente el sistema de numeración decimal se emplea en todo el mundo. Es muy raro encontrar algún pueblo o cultura en el que todavía se cuente de veinte en veinte o de cinco en cinco. Tal vez conozcas la numeración romana, no te confundas porque también es numeración decimal, aunque se escriban los números de otra manera. Las cifras que empleamos en los números son las cifras arábigas, se llaman así porque fueron los árabes los que extendieron su uso por Europa, pero en realidad provienen de la India. 0, 1, 2, 3, 4, 5, 6, 7, 8, 9.

EJERCICIOS DE SUMAS

Copia en el cuaderno las siguientes sumas y resuélvelas.

EJERCICIOS DE RESTAS

PROBLEMAS DE SUMA Y RESTA

Recuerda los pasos para resolver un problema correctamente:

1. Leer y entender el problema.

2. Analizar los datos que se tienen.

3. Comprender los datos que se buscan.

4. Hacer las operaciones necesarias.

5. Identificar el resultado o elemento faltante para resolver el problema.

1. En un cuartel había 85.400 soldados, si salieron a desfilar 34.257. ¿Cuántos soldados quedaron en el cuartel?

2. Miguel ahorró durante tres meses para comprar una bicicleta. En el primer mes ahorró 26.532 pesos, en el segundo mes ahorró 19.540 pesos y en el tercer mes ahorró 30.500 pesos. Si la bicicleta cuesta 150.000 pesos, ¿cuánto le falta para completar la cantidad necesaria?

3. Un alfarero tiene que hornear 550 ollas en tres semanas; si en la primera semana horneó 175 y la segunda 164, ¿cuántas ollas deberá hornear la tercera semana?

4.Alejandro tiene 6.000 canicas y como se va a ir a vivir a Bogotá le va a regalar a sus amigos 3.850 canicas. ¿Cuántas canicas le quedaran?

5.Toño compró un computador a credito y pagó  350.600 el primer mes, al mes siguiente 187.900 y queda debiendo

 280.500 ¿Cuánto cuesta el computador?

  

PROBLEMAS

EL PERÍMETRO

Calcular el perímetro cuando se conoce la longitud de un lado. Recuerda la fórmula del perímetro de un cuadrado. Para un cuadrado cuya longitud es L, el perímetro es simplemente cuatro veces la longitud del lado: P=4L. Determina la longitud de un lado y multiplícala por 4 para hallar el perímetro.

1. Hallar el perimetro al siguiente rectangulo:

2. Hallar el perimetro del cuadrado:

3. Halar el perímetro deL ROMBO:

MULTIPLICACIÓN POR DOS CIFRAS

 Hoy vas a aprender a resolver una multiplicación de 2 cifras ¡seguro que te resulta muy sencillo!

Antes de empezar, vamos a recordar cuáles son los términos de una multiplicación:

• FACTORES: son los números que multiplicas dentro de la multiplicación.

Dentro de los factores encontramos el:

Multiplicando: es el número que colocamos en la parte posterior de la multiplicación

Multiplicador: es el número que colocamos debajo del multiplicando.

• PRODUCTO: es el resultado de tu multiplicación y se sitúa en la parte inferior de la multiplicación.

El primer paso de tu multiplicación de 2 cifras es igual a hacer una multiplicación con una cifra.

• Multiplicamos las unidades del multiplicador por las cifras del multiplicando, el resultado de esta multiplicación lo ponemos en la fila de abajo. Tienes que ir número por número, y recuerda, siempre en orden de derecha a izquierda
•     

• Primero multiplicamos 5 x 1, el resultado de esta multiplicación es 5. Lo ponemos justo debajo de las Unidades.

  Después multiplicamos 5 x 8, el resultado de esta multiplicación es 40, ponemos el cero debajo de las decenas y recordamos que nos llevamos 4 para la siguiente multiplicación.

  Por último multiplicamos 5 x 7, el resultado de esta multiplicación es 35, pero recuerda que te llevabas 4 de la anterior multiplicación, por lo que el resultado final es 35 + 4 = 39, lo colocamos debajo de las centenas.

  Ya tienes la primera parte de la multiplicación, ahora vamos a por la segunda:
• Multiplicamos las decenas del multiplicador por las cifras del multiplicando, el resultado de esta multiplicación lo ponemos en la fila de abajo, pero desplazado una posición a la izquierda. Aquí también tienes que ir número por número y siempre realizamos la multiplicación de derecha a izquierda:
• 
• Ahora multiplicamos 9 x 8, el resultado de esta multiplicación es 72,  escribimos el 2 debajo del 9 y nos llevamos 7.
• 
• Por último, para terminar esta parte de la multiplicación, multiplicamos 9 x 7, el resultado de esta multiplicación es 63, pero recuerda que te llevabas 7 de la multiplicación anterior, por lo que el resultado es 63 +  7 = 70.  Lo colocamos debajo del 3.
  El último paso para terminar tu multiplicación es la suma.
• Ahora tenemos que sumar los productos que nos han dado en la multiplicación.
• 
• Ya tienes tu multiplicación,  ¿fácil verdad?
  ¡Ahora te toca practicar en casa! 
• NÚMEROS PARES E IMPARES
• Los números pares se pueden dividir exactamente en grupos de dos. El número cuatro se puede dividir en dos grupos de dos. Los números pares siempre terminan con un dígito de 0,2,4,6 u 8.
  2,4,6,8,10,12,14,16,18,20,22,24,26,28,30 son números pares.
  Los números impares NO se pueden dividir exactamente en grupos de dos. El número cinco se puede en dos grupos de dos y un grupo de uno.
  Los números impares siempre terminan con un dígito de 1,3,5,7, o 9.
  1, 3, 5, 7, 9, 11, 13, 15, 17, 19, 21, 23, 25, 27, 29, 31 son números impares.
  Ejercicio
  1.    Por medio de la división definir cuál número es par y cual es impar y justificar la respuesta

  1

  24

  17

  13

  100

  235

  2.    Construye números pares de 2 cifras completando
       4__  8____ 9___2___1_____3__________
  3.    Construye números impares de 3 cifras completando
  
  
  9___   2_____  8____  1_____  7___ 3____ 6_____  4____ 3________

LA DIVISIÓN

La división está presente en varios ámbitos de nuestra vida y podríamos definirla como una operación aritmética de descomposición que consiste en averiguar cuántas veces un número (el divisor) está contenido en otro número (el dividendo).

Podemos decir entonces que la división forma parte de la aritmética y es inversa a la multiplicación.

2- Términos de la división

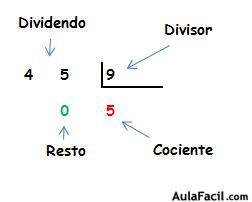
En una división de números naturales, sus términos se llaman dividendo y divisor y su resultado se llama cociente. Si la división no es exacta, se obtiene un resto que es menor que el divisor y distinto de cero.

- Dividendo: es el total que vamos a dividir.
- Divisor: es la cantidad por la cual se va a dividir al total.
- Cociente: es el resultado de la operación. Éste indica la cantidad der veces que el divisor “cabe” dentro del dividendo.
- Resto: es la parte que no se ha podido distribuir. Si el resto es diferente de cero, decimos que es una división inexacta.